La sphère d'al-Khidr

Pour le deuxième cycle du neuvième mois de la décade
comprenant la nuit et le jour :

Nous venons d'identifier al-Khidr à la figure ancestrale du Vivant – al-Ḥayy – et sa sphère au cycle adamantin qui est celui des prophètes.

Leur cycle s'étend sur 5.400 ans qui comptabilisent 64.000 lunaisons à raison de douze lunaisons synodiques par an.

Le nombre de ces lunaisons est celui des unités qui organisent la matrice arithmétique du kalpa dans laquelle s'inscrit le cycle de l'écliptique.

Les unités du kalpa sont des catégories abstraites qui s'appliquent indifféremment aux lunaisons de la sphère adamantine ou aux années du cycle de l'écliptique.

Les 25.920 ans du cycle de l'écliptique correspondent ici aux quatre dixième de la matrice arithmétique à partir desquels s'accomplit la quadrature du cercle.

La quadrature du cercle est une opération qui organise la décade en quatre parties décroissantes sur le modèle de ce que la tradition pythagorique appelle une tétraktys.

Pour parvenir à un nombre d'années qui correspondent à un nombre de lunaisons semblables aux unités de la matrice, nous avons donc subdivisé la sphère par dix.

Mais nous avons attribué aux cycles de la sphère des régimes différents qui varient au passage des deux derniers âges du cycle de l'écliptique.

Les âges du cycle de l'écliptique sont les yuga du manvatara qui organisent le temps du kalpa à partir de la tétraktys dans sa matrice arithmétique.

Nous avons donc subdivisé la sphère d'al-Khidr en six cycles de 6.000 lunaisons suivis de quatre cycles de six cents ans qui leur succèdent autour de ce passage.

Les cycles de lunaisons qui correspondent à celui du phénix forment un ensemble de 36.000 lunaisons qui rappellent les six jours de la création vétérotestamentaire.

Les cycles qui correspondent aux cohortes de l'âge de fer – ou à celles du kali yuga – laisse un solde résiduel de 192 ans qui correspond à la fin des temps.

Ce solde résiduel n'est pas pris en compte dans l'évocation de la sphère ; comme les jours complémentaires ne sont pas pris en compte par les temps apocalyptiques.

Douze mois de trente jours étant en effet comme autant d'années (360) sans prendre en compte le solde résiduel (5,242) des jours complémentaires de l'année.

Cette façon de voir ne doit pas être perçue comme une opération aléatoire puisque le nombre des années qui en résulte est celui des degrés dans un pentagone (540).

Ce pentagone s'inscrit alors dans un cercle qui contient la totalité de la manifestation cosmique et le regard métaphysique des prophètes sur sa réalité cyclique.

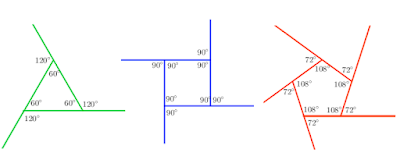
Les degrés de l'octogone (1.080) apparaissent comme une décade par rapport aux degrés des angles du pentagone (108) et comme un cercle (6) par rapport aux degrés des angles du triangle (180).

Ces rapports sont aussi ceux du nombre des classes d'âge (18) pour celui des degrés dans les angles de ce triangle (60) quand ils apparaissent comme une figure médiane avec le carré.

Les degrés du carré (360) sont en effet semblables à ceux du cercle (360) du point de vue des nombres et le nombre des années (90) pour celui des âges à celui des degrés (90) pour les angles de ce carré.

Les degrés du triangle (180) apparaissent alors comme la moitié d'un cercle du point de vue du nombre de ses degrés (360) et ceux du pentagone (540) comme un premier fractionnement par rapport à l'unité de cet ensemble.

Relevons enfin que les degrés de l’ennéagone (1.260) sont semblables aux années que l'Apocalypse de Jean accorde à ses deux témoins en multipliant cette unité (360) par un multiplicateur – « 3,5 x 360 = 1260 » et « 1.260 / 9 = 140° » pour chaque angle.

On peut également supposer que le septième jour de la semaine est sabbatique parce que le nombre sept est le seul nombre de la décade à ne pas être un quotient de cette unité de mesure.

●

« La présence d'une chose connue pour celui qui la connaît, qui est l'être même de la science du savant sur cette chose, n'est pas hors de ce dilemme : [ ... ]

« [ ... ] ou bien l'attribut essentiel de la chose est connu et dès lors il ne peut changer dans la chose connue, ou bien ce n'est pas son attribut essentiel qui est connu et dès lors, la chose est susceptible de changements. »

Cf. A. L. M. Nicolas – Essai sur le sheykhisme – La science de Dieu (1911)
   

Polygones réguliers	Degrés des radiants	Degrés des angles	Degrés des polygones
Circonférence	360°	0	0
Diamètre	180°	0	0
Triangle	120°	60°	180°
Carré	90°	90°	360°
Pentagone	72°	108°	540°
Hexagone	60°	120°	720°
►	51,428571 ... (3/7)	128,57142 ... (4/7)	899,99994 ...
Octogone	45°	135°	1 080°
Ennéagone	40°	140°	1 260°
Décagone	36°	144°	1 440°